DFS(Deep First Search)深度优先搜索。
BFS(Breath First Search)广度优先搜索。
今天想说一说个人对于这两个搜索方法的见解。在我看来,DFS与BFS是算法道路上最基础最容易掌握的,同时,又能提供巨大助力的方法之一。我这里斗胆用方法二字来形容DFS以及BFS,用搜索思想来囊括二者。方法是死的,而思想是活的,我们应该通过对这两种方法的剖析来获得这种思想,因为无论是在现实问题还是算法题目上,问题模型都是多变的,我们要着重于理解思想而后针对特定问题能用最佳的方法去解决。
话不多说,我们先从DFS说起。
1.DFS(深度优先搜索)
讲搜索当然不能撇开图,搜索思想在图问题中能以最直观的方式展现。下面是我个人对于DFS的理解与概括,如果你是初学者看不懂可以结合后面举的例子来理解,如果对于我的总结哪里有不对的地方欢迎私信指正我。
深度优先搜索的步骤分为 1.递归下去 2.回溯上来。顾名思义,深度优先,则是以深度为准则,先一条路走到底,直到达到目标。这里称之为递归下去。
否则既没有达到目标又无路可走了,那么则退回到上一步的状态,走其他路。这便是回溯上来。
下面结合具体例子来理解。
如图所示,在一个迷宫中,黑色块代表玩家所在位置,红色块代表终点,问是否有一条到终点的路径
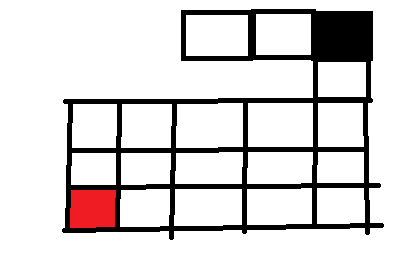
我们用深度优先搜索的方法去解这道题,由图可知,我们可以走上下左右四个方向,我们规定按照左下右上的方向顺序走,即,如果左边可以走,我们先走左边。然后递归下去,没达到终点,我们再回溯上来,等又回溯到这个位置时,左边已经走过了,那么我们就走下边,按照这样的顺序与方向走。并且我们把走过的路标记一下代表走过,不能再走。
所以我们从黑色起点首先向左走,然后发现还可以向左走,最后我们到达图示位置
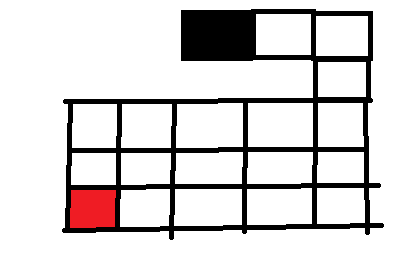
已经连续向左走到左上角的位置了,这时发现左边不能走了,这时我们就考虑往下走,发现也不能走,同理,上边也不能走,右边已经走过了也不能走,这时候无路可走了,代表这条路是死路不能帮我们解决问题,所以现在要回溯上去,回溯到上一个位置,
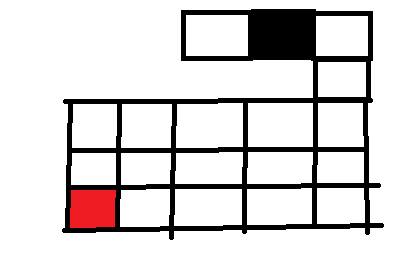
在这个位置我们由上可知走左边是死路不行,上下是墙壁不能走,而右边又是走过的路,已经被标记过了,不能走。所以只能再度回溯到上一个位置寻找别的出路。

最终我们回溯到最初的位置,同理,左边证明是死路不必走了,上和右是墙壁,所以我们走下边。然后递归下去
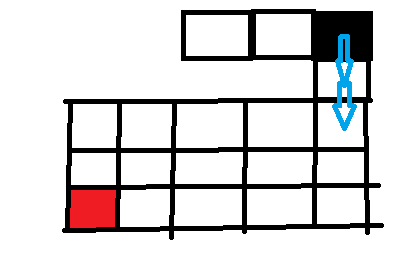
到了这个格子,因为按照左下右上的顺序,我们走左边,递归下去
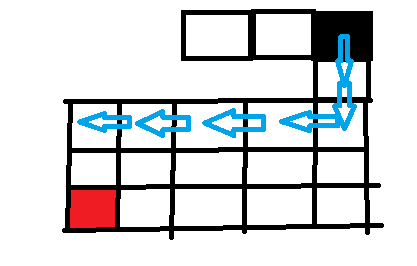
一直递归下去到最左边的格子,然后左边行不通,走下边。
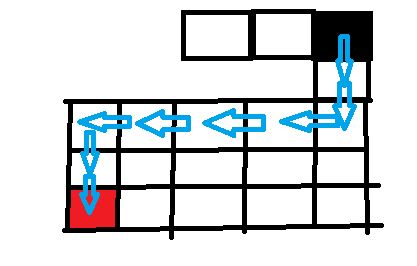
然后达到目标。DFS的重要点在于状态回溯。代码如下
int goal_x = 9, goal_y = 9; //目标的坐标,暂时设置为右下角
int n = 10 , m = 10; //地图的宽高,设置为10 * 10的表格
int graph[n][m]; //地图
int used[n][m]; //用来标记地图上那些点是走过的
int px[] = {-1, 0, 1, 0}; //通过px 和 py数组来实现左下右上的移动顺序
int py[] = {0, -1, 0, 1};
int flag = 0; //是否能达到终点的标志
void DFS(int graph[][], int used[], int x, int y)
{
// 如果与目标坐标相同,则成功
if (graph[x][y] == graph[goal_x][goal_y]) {
printf("successful");
flag = 1;
return ;
}
// 遍历四个方向
for (int i = 0; i != 4; ++i) {
//如果没有走过这个格子
int new_x = x + px[i], new_y = y + py[i];
if (new_x >= 0 && new_x < n && new_y >= 0
&& new_y < m && used[new_x][new_y] == 0 && !flag) {
used[new_x][new_y] = 1; //将该格子设为走过
DFS(graph, used, new_x, new_y); //递归下去
used[new_x][new_y] = 0;//状态回溯,退回来,将格子设置为未走过
}
}
}
2.BFS(广度优先搜索)
广度优先搜索较之深度优先搜索之不同在于,深度优先搜索旨在不管有多少条岔路,先一条路走到底,不成功就返回上一个路口然后就选择下一条岔路,而广度优先搜索旨在面临一个路口时,把所有的岔路口都记下来,然后选择其中一个进入,然后将它的分路情况记录下来,然后再返回来进入另外一个岔路,并重复这样的操作,用图形来表示则是这样的,例子同上
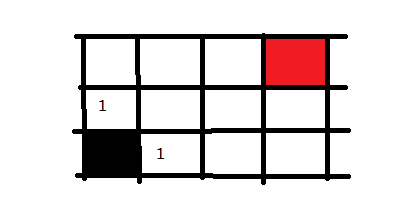
从黑色起点出发,记录所有的岔路口,并标记为走一步可以到达的。然后选择其中一个方向走进去,我们走黑点方块上面的那个,然后将这个路口可走的方向记录下来并标记为2,意味走两步可以到达的地方。
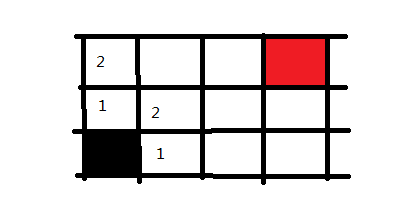
接下来,我们回到黑色方块右手边的1方块上,并将它能走的方向也记录下来,同样标记为2,因为也是走两步便可到达的地方
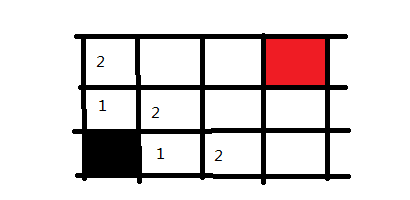
这样走一步以及走两步可以到达的地方都搜索完毕了,下面同理,我们可以迅速把三步的格子给标记出来
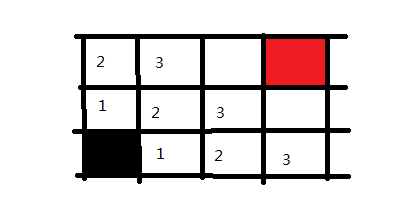
再之后是四步,五步。

我们便成功寻找到了路径,并且把所有可行的路径都求出来了。在广度优先搜索中,可以看出是逐步求解的,反复的进入与退出,将当前的所有可行解都记录下来,然后逐个去查看。在DFS中我们说关键点是递归以及回溯,在BFS中,关键点则是状态的选取和标记。
代码如下
int n = 10, m = 10; //地图宽高
void BFS()
{
queue que; //用队列来保存路口
int graph[n][m]; //地图
int px[] = {-1, 0, 1, 0}; //移动方向的数组
int py[] = {0, -1, 0, 1};
que.push(起点入队); //将起点入队
while (!que.empty()) { //只要队列不为空
auto temp = que.pop(); //得到队列中的元素
for (int i = 0; i != 4; ++i) {
if(//可以走) {
//标记当前格子
//将当前状态入队列,等待下次提取
}
}
}
}
注:以上两个代码只是提供思路,并非是语法正确的可运行代码。
3.总结
对于这两个搜索方法,其实我们是可以轻松的看出来,他们有许多差异与许多相同点的。
1.数据结构上的运用
DFS用递归的形式,用到了栈结构,先进后出。
BFS选取状态用队列的形式,先进先出。
2.复杂度
DFS的复杂度与BFS的复杂度大体一致,不同之处在于遍历的方式与对于问题的解决出发点不同,DFS适合目标明确,而BFS适合大范围的寻找。
3.思想
思想上来说这两种方法都是穷竭列举所有的情况。